Simulación de sistemas en Excel: ¿cómo aplicar dinámica de sistemas?

¡Bienvenida/o a una nueva entrada del blog de Atlas Consultora! En la nota de hoy veremos cómo trasladar nuestros análisis cualitativos para realizar simulación de sistemas en Excel.

Estamos terminando un ciclo de artículos en los que analizamos diferentes herramientas para tomar decisiones que mejoren la competitividad. Hoy nos dedicaremos a dar cierre a la temática sobre la que hablamos las últimas 2 semanas:

1. Cómo estudiar la dinámica de sistemas complejos,
2. Cómo utilizar los diagramas de flujo, stock y bucles causales para entender mejor estos problemas.

Primero, veremos algunos de los resultados que podemos obtener cuando analizamos sistemas complejos. A continuación, abordaremos la simulación de sistemas en Excel, como forma de aplicación de lo aprendido. Por último, analizaremos los puntos a favor y en contra de este tipo de herramientas.

---

Modos fundamentales del comportamiento dinámico

Ya hemos aprendido que la estructura de un sistema se puede modelar como un ciclo de interacciones y retroalimentación. También, sabemos que esos ciclos se pueden representar mediante diagramas conceptuales. Por otro lado, observamos que la variedad de sistemas y comportamientos a nuestro alrededor es asombrosa e inabarcable. Con eso en mente, podríamos pensar que los posibles comportamientos de un sistema dinámico son infinitos. Sin embargo, la mayoría de los sistemas se comportan de acuerdo a modos ya conocidos y analizados.

¿Querés aplicar mejora continua en tu organización?
Descarga ahora la plantilla A3 PDCA Atlas y aplicá la metodología

Existen 6 modos fundamentales para el comportamiento que se obtienen en la simulación de sistemas. Podemos ver un diagrama de estos comportamientos en la siguiente figura:

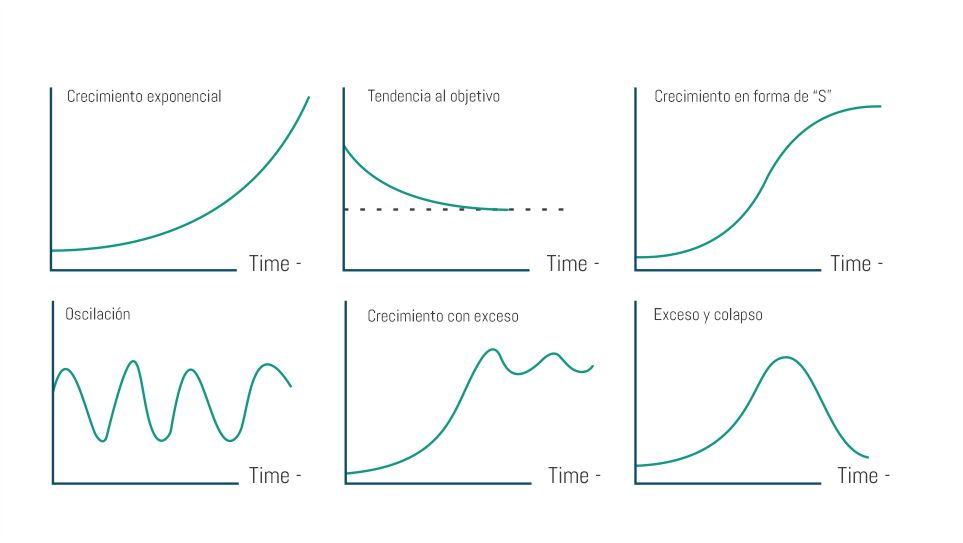
A continuación, vamos a analizar los 3 casos más comunes.

1. Crecimiento exponencial

Este es el resultado de un bucle con retroalimentación positiva. Es decir: un cambio de la variable independiente genera un cambio en el mismo sentido de la variable dependiente. Podemos ver el diagrama de bucle causal correspondiente en la siguiente figura:

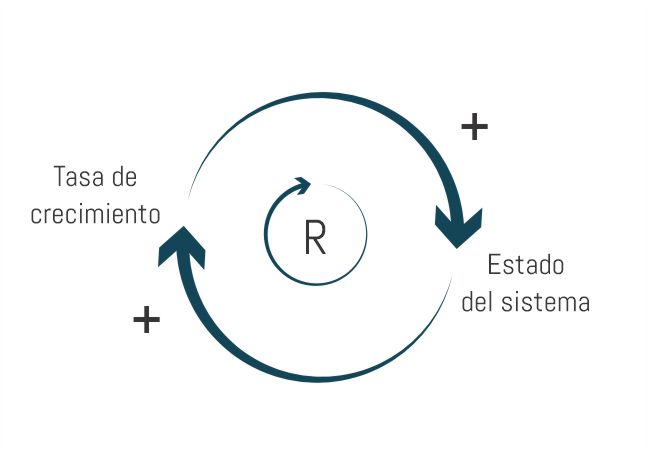
Un caso muy claro para ejemplificar es el crecimiento de una población. Dada una población, podemos identificar su tasa de crecimiento como la cantidad de personas que nacen cada cierto tiempo. A medida que pase el tiempo, y la base de población crezca, mayor será la tasa de crecimiento.

El punto interesante de este comportamiento es que el “período de duplicación” se mantiene constante en el tiempo. Esto significa que la población se duplica cada X unidades de tiempo, siempre.

Por último, vale aclarar que este mismo efecto puede darse para casos de decrecimiento, donde un evento desencadena una caída en picada. El ejemplo clásico para este comportamiento es la caída de una acción o de la bolsa.

2. Tendencia al objetivo

Este es el resultado de un bucle con retroalimentación negativa. Es decir: un cambio de la variable independiente genera un cambio con sentido contrario de la variable dependiente. Este tipo de bucles logra un balance o equilibrio en el sistema, buscando alcanzar un estado deseado. Podemos ver el diagrama de bucle causal correspondiente en la siguiente figura:

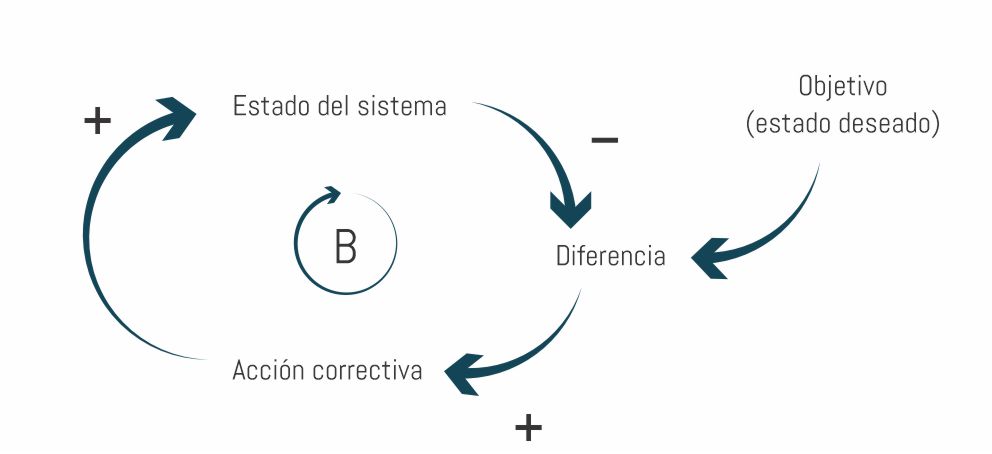
Un caso típico de este comportamiento se da al implementar programas de gestión de la calidad. Generalmente, la cantidad de defectos generados bajará muy rápido al principio. Sin embargo, cada vez será más difícil seguir mejorando. Por eso, luego de un tiempo la cantidad de defectos encontrados se estabilizará.

3. Oscilación

Este es el resultado de un bucle con retroalimentación negativa en el cual existen demoras significativas. Al igual que en el caso anterior, el sistema tiene definido un objetivo. Sin embargo, en este caso la retroalimentación, la decisión y sus efectos no son inmediatos. Este es uno de los tipos más comunes de comportamientos que se pueden observar. Podemos ver el diagrama de bucle causal correspondiente en la siguiente figura:

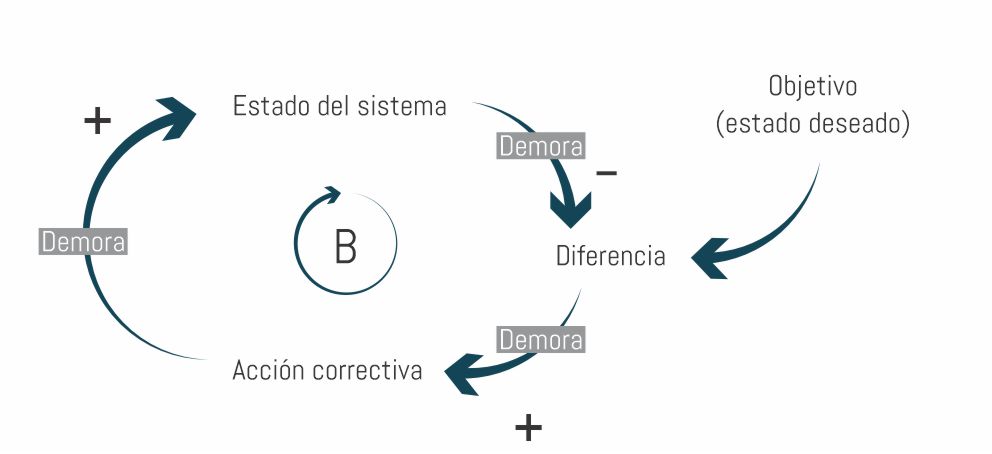
Un caso típico de este comportamiento es el control de temperatura del aire acondicionado. Al principio, la temperatura del ambiente es superior a lo que deseamos. Entonces, prendemos el equipo y esperamos. Luego de un tiempo es muy posible que la temperatura haya bajado demasiado, y decidiremos apagarlo. Finalmente, luego de cierto tiempo, deberemos prenderlo nuevamente.

Simulación de sistemas en Excel

Ahora que ya tenemos en mente los potenciales resultados que podemos encontrar, abordaremos la simulación de un sistema en Excel. Para nuestro ejemplo, utilizaremos un sistema relativamente sencillo y muy fácil de imaginar: una granja de pollos. En este sistema, buscaremos simular el comportamiento de la población de pollos de nuestra granja. ¡Comencemos!

Paso 1. El dilema del huevo y el pollo

Vamos a considerar una situación sencilla: una granja de pollos. Comenzaremos con una cantidad de huevos determinada, y algunos de esos huevos se convertirán en pollos. Esos pollos pondrán más huevos, que luego se convertirán en más pollos, y así. El diagrama causal que representa este sistema sería algo como lo que vemos en esta imagen:

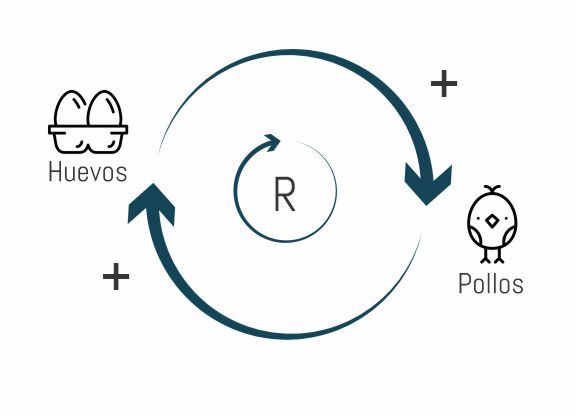
Para darle un poco más de información al modelo, podemos asumir:

• Comenzaremos con 10 huevos y ningún pollo.
• Cada pollo pone 5 huevos por semana en promedio (tasa de producción de huevos).
• Los huevos tardan 3 semanas en convertirse en pollos.
• 20% de todos los huevos se convierten en pollos (tasa de nacimientos). El resto se venden como huevos.

A partir de estos supuestos, podemos armar nuestro diagrama de flujos y stock, que debería resultar más o menos así:

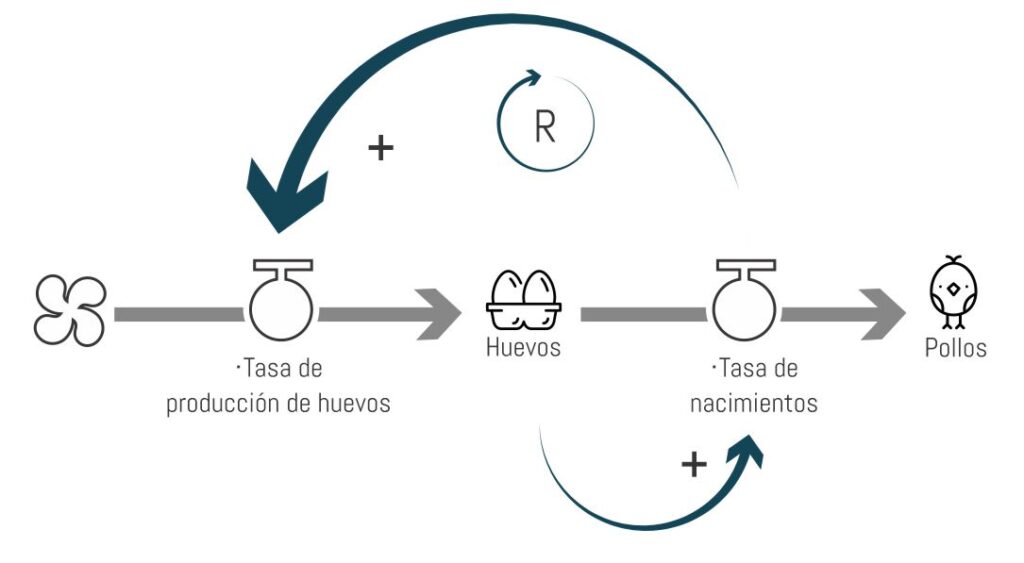
Finalmente, debemos llevar esta información a una hoja de cálculo. Para lograrlo, necesitaremos explicitar las relaciones entre las variables mediante fórmulas:

• La cantidad de huevos que se ponen cada semana (Ch), que depende de la cantidad de pollos (Cp) y de la tasa de producción (Tp). Nh = Cp * Tp.
• La cantidad de pollos que nacen cada semana (Cn), que depende de los huevos puestos hace 3 semanas (Ch-3) y de la tasa de nacimientos (Tn). Cn = Ch-3 * Tn.

Ya tenemos suficiente información para armar nuestra simulación de este sistema en Excel, y eso es lo que hicimos. Si querés ver el detalle de cómo lo armamos, aquí podés consultar una copia del documento. Lo más interesante sin embargo es el gráfico de comportamiento en el tiempo que obtenemos para este sistema: un claro ejemplo de crecimiento exponencial.

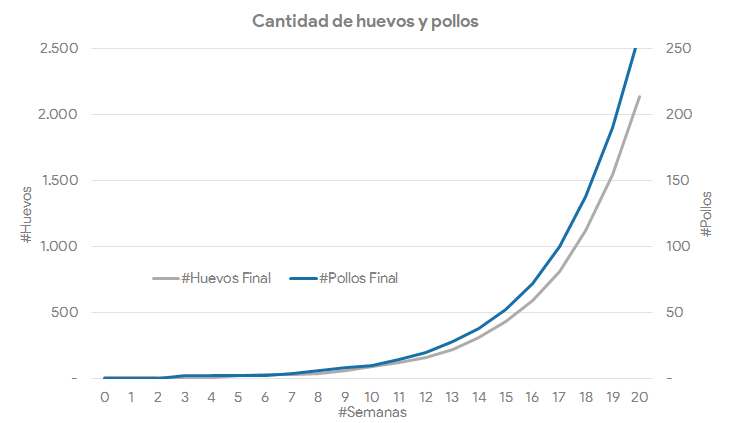
Paso 2. ¡Cuidado con los autos!

¿Por qué el pollo cruzó el camino? Nadie lo sabe, y a ellos no les interesa contarnos. Sin embargo, lo que sí sabemos es que les gusta cruzar la ruta. También sabemos que no son particularmente habilidosos para esa tarea, así que muchos de ellos no sobreviven a la aventura. Hemos encontrado entonces un nuevo factor que interviene en nuestro sistema: la tasa de expiración (Te) de pollos. Si introducimos este nuevo concepto en nuestro diagrama causal, nos queda algo así:

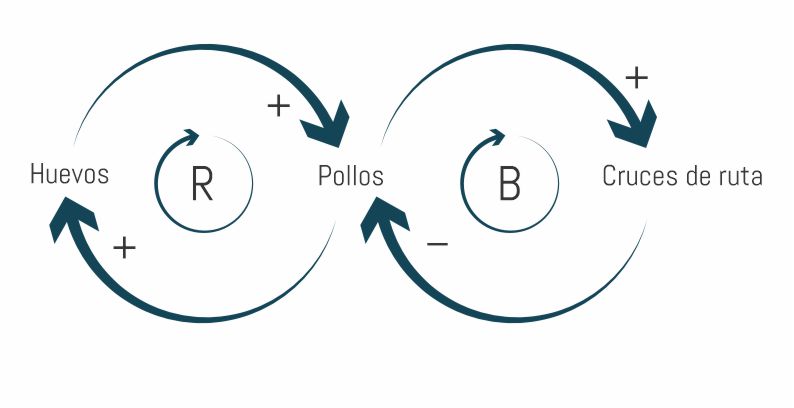
Al igual que en el caso anterior, debemos dar un poco más de detalle respecto al comportamiento del sistema para seguir avanzando. Vamos a plantear entonces algunos supuestos adicionales:

• El 50% de los pollos cruzan la ruta, sufren un accidente y no sobreviven. Esta es la tasa de expiración (Te) de pollos en nuestra granja. El resto de los pollos continúan sanos y salvos.

A partir de estos supuestos, podemos armar un nuevo diagrama de flujos y stock, que debería resultar más o menos así:

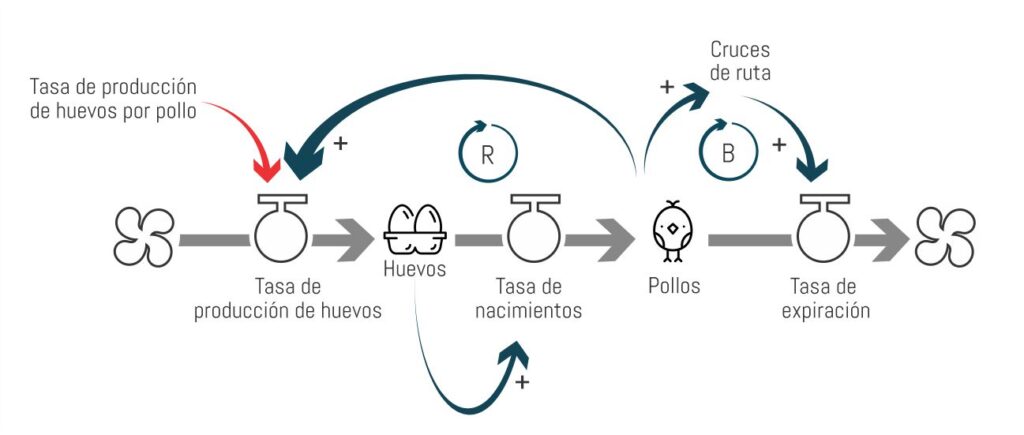
Finalmente, debemos llevar esta información a una hoja de cálculo. Para lograrlo, necesitaremos explicitar las relaciones entre las variables mediante fórmulas:

• La cantidad de pollos que perdemos cada semana (Cm) depende de la cantidad de pollos al inicio de la semana (#Pollos inicio), y de la tasa de expiración (Te). Cm = #Pi * Te.
• Todo lo demás se mantiene sin cambios.

Simulemos ahora el sistema y veamos qué pasa. La hoja de cálculo completa se puede descargar desde aquí. En este caso, vemos mucha oscilación, pero sigue siendo un crecimiento exponencial:

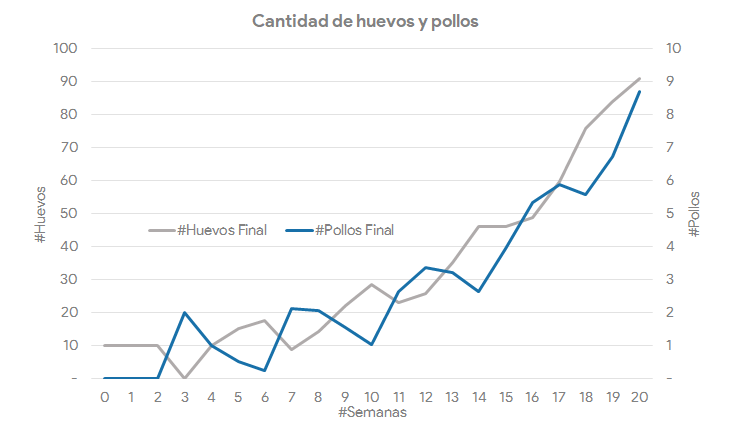
Sin embargo, si cambiamos la tasa de nacimiento (Tn) a 15% y la tasa de expiración (Te) a 70%, el comportamiento de nuestro sistema tiende al equilibrio:

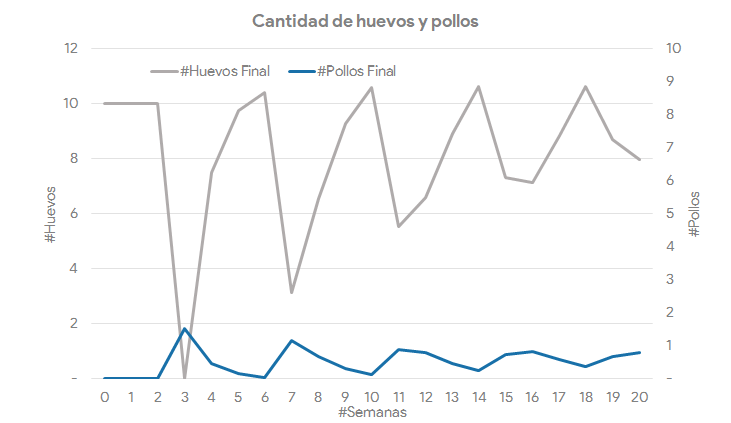
Paso 3. Es hora de gestionar

El último escenario que vamos a analizar es aquel donde decidimos intervenir el sistema. En este caso, vamos a introducir un objetivo de cantidad de pollos a mantener en nuestra granja, ya que no tenemos espacio ni alimento infinitos. Para eso, cada semana compararemos la cantidad de pollos con nuestro objetivo y luego tomaremos una decisión. Esa decisión será sobre la tasa de nacimientos (vender más o menos huevos), para ajustar el la población futura de pollos. Si llevamos este nuevo concepto a un diagrama de flujos y stock, tendremos algo así:

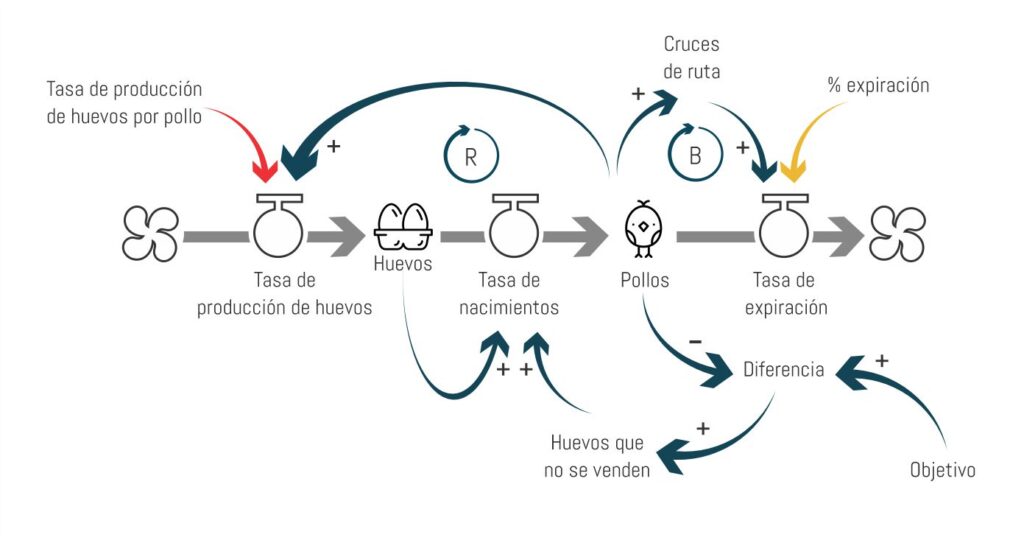
Antes de volver a la hoja de cálculo, debemos establecer nuestro objetivo, y definir las reglas de decisión. Vamos a fijar nuestro objetivo para la población en 25 pollos al final de cada semana. Además, de acuerdo a la diferencia observada, tomaremos las siguientes decisiones:

• Si tenemos 22 pollos o menos, la tasa de nacimiento será de 15%.
• Cuando haya entre 22 y 28 pollos, la tasa de nacimientos será de 10%.
• Por último, cuando tengamos más de 28 pollos la tasa de nacimientos será de 2%.

Llevamos este nuevo modelo de decisión a nuestra simulación de sistemas, y obtenemos el siguiente comportamiento esperado:

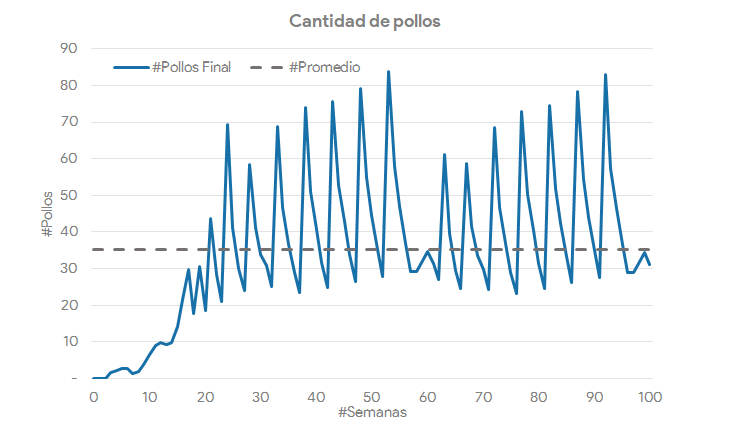
Se puede apreciar fácilmente que con este set de reglas para tomar decisiones estamos generando un comportamiento oscilatorio. No solo sino, sino que además no nos acercamos a nuestros objetivo, ni siquiera en el promedio. Al problema aquí no está solamente en los valores de las decisiones, sino que además tenemos cambios muy bruscos y muy frecuentes. Veamos entonces cómo podemos mejorar nuestro modelo.

Paso 4. Es hora de gestionar (pero bien)

El principal problema con tomar decisiones repentinas y con demasiada frecuencia es que tendemos a caer en la trampa del pensamiento lineal y las soluciones miopes. Si pretendemos lograr un sistema cuyo comportamiento sea suave y estable, nuestras decisiones tienen que serlo también.

Entonces, ahora vamos a probar algo diferente: en lugar de mirar solamente las existencias actuales, vamos a mriar todo nuestro “pipeline“. Esto significa tener en cuenta no solo la cantidad de pollos vivos, sino también aquellos que esperamos que nazcan, y también los que morirán. Además, vamos a ampliar nuestro rango para tomar decisiones, apuntando a generar un flujo continuo de pollos.

Si introducimos estos nuevos conceptos en nuestro modelo de simulación de sistemas, y jugamos un poco con los valores de las decisiones, podremos obtener algo como esto:

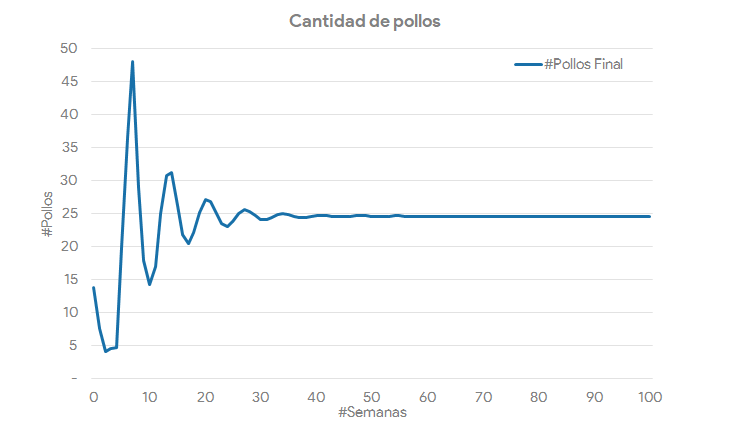
Resumen y consideraciones

El de hoy ha sido un largo viaje, así que gracias (y felicitaciones) por llegar hasta aquí. Repasemos un poco: comenzamos analizando los comportamientos fundamentales de la simulación de sistemas y sus significados e implicancias. Luego, nos abocamos a realizar una simulación de sistemas en Excel, con el ejemplo de la granja de pollos. Allí vimos cómo los sistemas se complejizan y cambian su comportamiento cuando empezamos a sumar variables. Además, analizamos lo sensibles que pueden ser a pequeños cambios.

Uno de los aspectos fundamentales que espero te lleves de esta nota es que debemos evitar reglas demasiado rígidas y fijar límites de control consistentes con nuestros objetivos. Por eso, si queremos lograr sistemas estables, debemos tomar decisiones que también lo sean. Si seguimos este lineamiento, y evitamos el camino de las soluciones miopes, estaremos encaminados a una excelente gestión.

Esto es todo por hoy. En la nota de la semana que viene analizaremos otro tipo de herramientas para realizar simulación de sistemas, y cerraremos esta serie analizando los pros y contras al momento de utilizar estas herramientas para la gestión de las organizaciones.