Colas de espera: modelos y fundamentos

Esta es la segunda de nuestra serie de notas conectada a entender y gestionar las colas de espera en nuestra organización. Si todavía no lo hiciste podes leer la primera haciendo click acá.

De dónde surge el modelo de colas de espera

La semana pasada tuvimos una introducción a los aspectos centrales para gestionar colas de espera. De esta manera pudimos entender y modelar dichas situaciones. En estas contamos con cierta población de agente de personas, productos, información. Las mismas arriban con cierta distribución en sus tiempos de llegada. Luego de la llegada forman colas de espera. Éstas se rigen mediante una disciplina de prioridad, como por ejemplo primero Entra Primero Sale.

¿Querés aplicar mejora continua en tu organización?
Descarga ahora la plantilla A3 PDCA Atlas y aplicá la metodología

La instalación de servicio a la cual arriban está formada por servidores (personas, máquinas) que brindan un servicio con cierta distribución de tiempos de atención.

Para representar estos modelos introdujimos la notación de Kendall, con la forma 1/2/3, siendo cada uno de estos componentes: la distribución de llegadas, la distribución de servicio y el número de servidores, respectivamente.

En la nota de esta semana buscaremos profundizar en los aspectos a tener en cuenta a la hora de dimensionar nuestra instalación de servicio, a partir de entender cuáles son las lógicas que rigen a las filas en el caso de canales y servidores únicos, para poder responder a las preguntas como:

¿Podremos satisfacer una demanda mayor con nuestro servicio actual?
¿Cuánto deberán esperar los clientes en esta nueva situación?
¿Cómo y cuánto podremos disminuir los tiempos de espera en nuestras filas?
¿Cuál es la máxima demanda que podremos abastecer?
¿Como gestionar colas de espera?

---

También te podrían interesar los siguientes artículos 📝

---

Cuáles son los parámetros de un modelo de colas de espera.

En la nota anterior, vimos las estructuras típicas de los procesos de servicio. Hoy tomaremos como punto de partida la más simple de ellas: solo un canal-camino posible, de una única fase-etapa, con una distribución de llegadas Poisson (M), una distribución de tiempos de servicio exponencial (M) y una lógica de atención primero llega-primero se atiende (PEPS o FIFO) donde los agentes esperan hasta ser atendidos (pacientes). Este modelo, en notación de Kendall M/M/1, nos servirá de base para los casos más complejos:

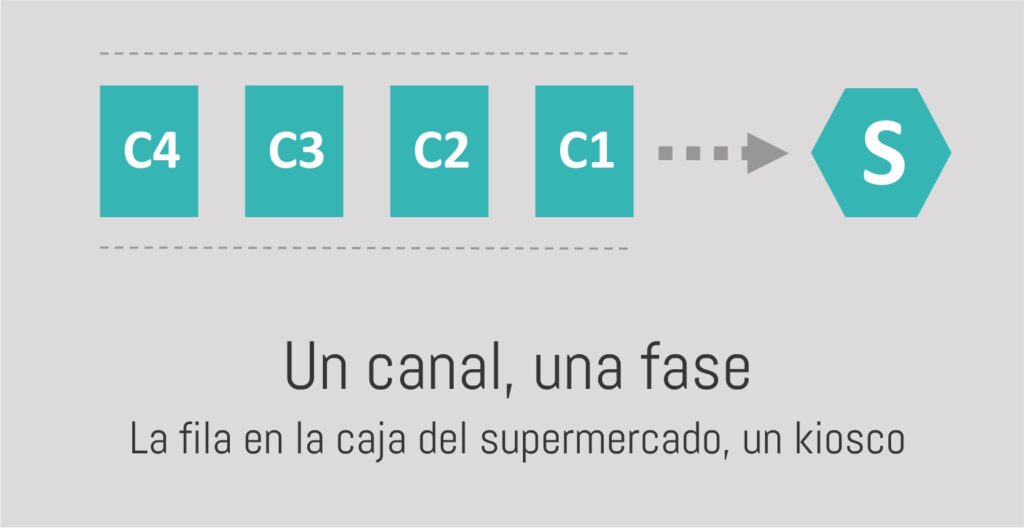
Para poder describir este tipo de filas deberemos entender algunos conceptos.

Tasa de llegadas (λ)

Nos da información del ritmo promedio con el que llegan los agentes a nuestra fila, lo que es indicativo de la demanda que tenemos en cierto proceso, medido en agentes por unidad de tiempo. La inversa de esta es el tiempo entre llegadas (1/λ).

Tasa de servicio (μ)

Nos habla del ritmo promedio al que se atiende a los agentes presentes en la fila, indicativo de la capacidad de nuestro sistema, también medido en agentes por unidad de tiempo. A la inversa se la conoce como tiempo de servicio (1/μ).

Utilización (ρ = λ/μ)

es indicativo de la proporción del tiempo en que el servidor está ocupado.

Largo promedio de la fila (L_q)

El número de clientes o productos esperando a ser atendidos, en promedio.

Tiempo promedio en la fila (W_q)

El promedio del tiempo que cada cliente o producto pasa en la fila. Por ley de Little (W_q = L_q/λ), vemos que el tiempo promedio que cada agente espera es directamente proporcional al largo de la fila.

Largo de la fila y el tiempo de espera: cómo actúa el efecto de la tasa de servicio y de llegadas en modelos de colas de espera

Existen numerosas herramientas para facilitar el cálculo de estos modelos. En el Sandbox de más abajo podremos visualizar el efecto en el largo de la fila a partir de variar: el número de clientes iniciales (initial number of customers), el tiempo medio entre llegadas (mean time between arrivals) y el tiempo medio de servicio (mean service time) con un nivel de variabilidad del servicio dado (σ_s):

Conclusión de experimentar con distintos valores

• Independientemente de la cantidad de clientes iniciales, si el tiempo de servicio es menor al tiempo entre llegadas (1/μ > 1/λ, equivalente a μ < λ) la fila (y por ende el tiempo de espera; recordemos W_q = L_q/λ) crece indefinidamente.

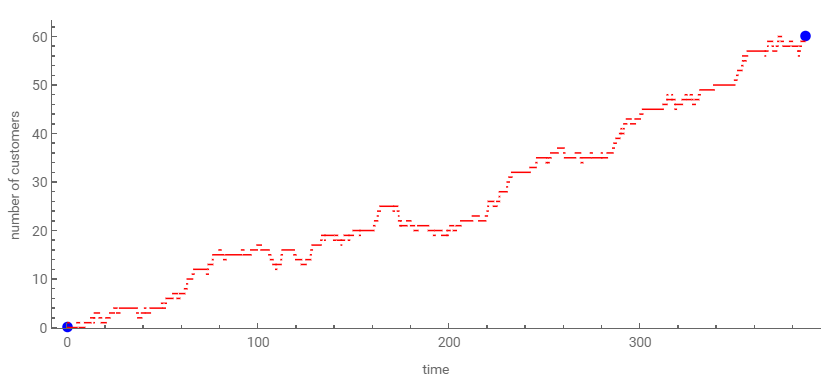
• Si el tiempo de servicio es menor al tiempo entre llegadas (1/μ < 1/λ, equivalente a μ > λ), la fila variará en forma acotada. Cuanto mayor sea la tasa de servicio y que la de llegadas, la fila tomará valores menores, tanto pico como promedio.

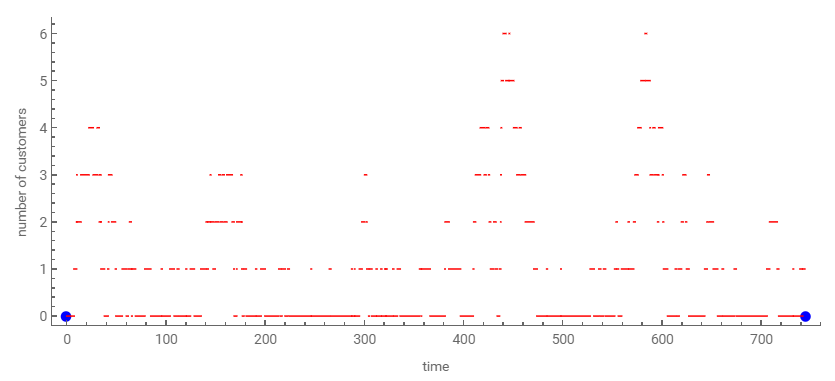
• En todos los casos, existe una primera etapa transitoria hasta que el modelo que simulamos alcanza un régimen estable o permanente. Este aspecto lo veremos con mayor profundidad al ver simulación.

para que nuestro sistema funcione en forma estable, es decir que la fila y tiempo de espera no crezcan indefinidamente, en promedio el ritmo al que atendemos deberá ser mayor al ritmo de llegada de los agentes a nuestro sistema.

El largo de la fila versus la variabilidad de los tiempos de servicio

Además del ritmo medio de atención, el largo de la fila y tiempo de espera en la misma se verán afectados por el nivel de variabilidad dicho ritmo de atención. Para entender este punto, analizaremos la expresión general del largo de una fila, en función de la tasa de llegadas (λ), la tasa de servicio (μ) y la variabilidad del tiempo de servicio (a partir de la desviación estándar del mismo; σ_s). Esta expresión será válida para valores de λ/μ< 1, es decir para un sistema estable:

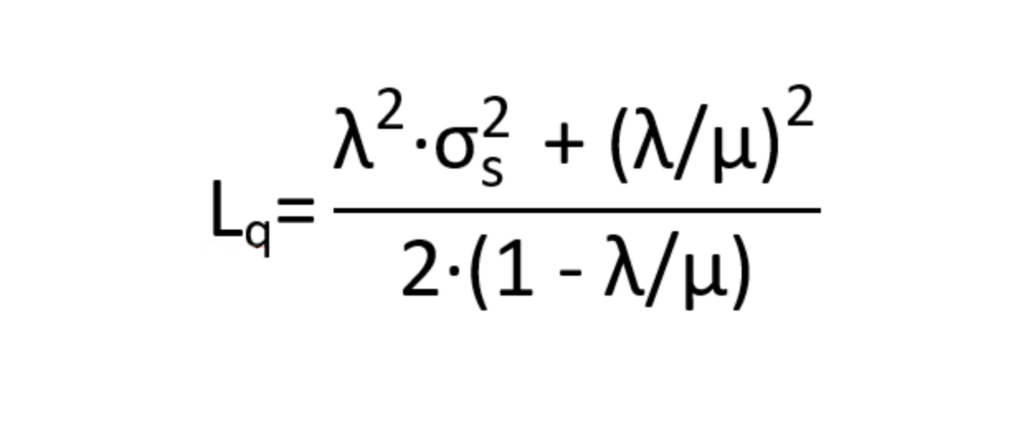
Dados ciertos valores de tasa de servicio y de llegadas, el largo de la fila aumenta con el aumento de la variabilidad del tiempo de servicio (σ_s).

Comparación de tiempos de servicios

A modo de ejemplo, compararemos dos casos tipo para un único servidor y una fase: uno con una distribución de tiempos servicio exponencial (σ_s=1/μ) utilizada como referencia para describir gran variedad de procesos de la realidad con componentes de variabilidad, versus una distribución de tiempos de servicio constante (σ_s=0) utilizada para representar procesos automáticos y repetitivos dónde no existe variabilidad.

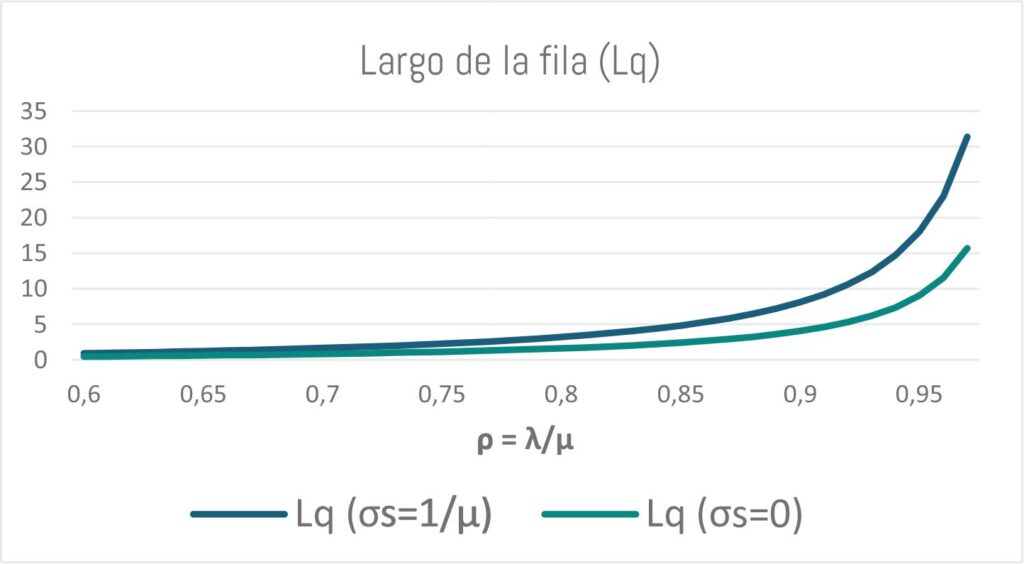
De este gráfico podemos sacar ciertas conclusiones:

• Conforme la utilización (ρ = λ/μ) se aproxima a 1, el largo de la fila se dispara rápidamente, conectado con el límite en el que el sistema puede funcionar en forma estable.
• A valores similares de utilización, un servicio con menor variabilidad tendrá menores filas (y esperas), pudiendo reducir hasta la mitad la fila en el caso límite de lograr eliminar completamente la variabilidad (σ_s=0).

Para un mismo ritmo medio de atención, trabajar en estandarizar y reducir la variabilidad de nuestros procesos nos servirá para reducir las filas y minimizar los tiempos al gestionar las esperas.

Modelo de varios servidores conectados para gestionar las colas de espera.

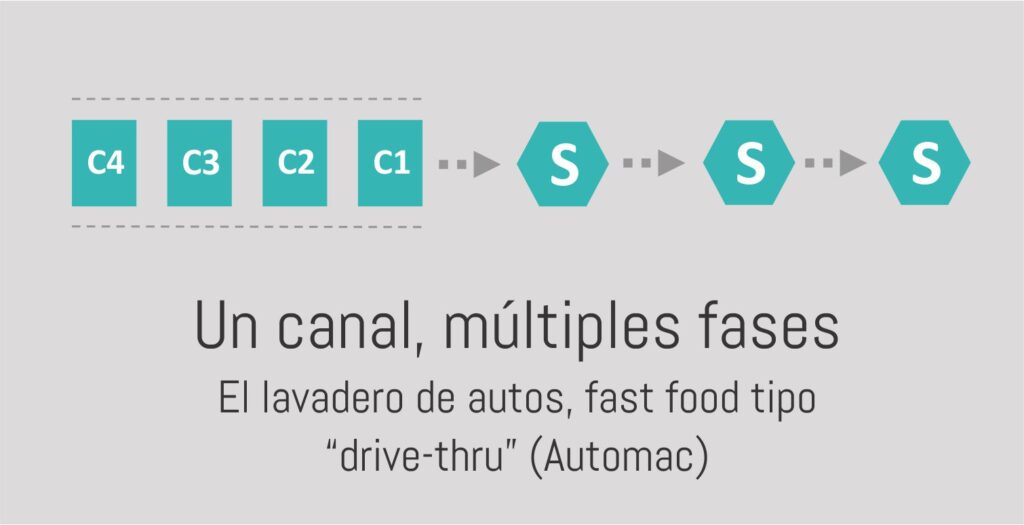
Este tipo de sistemas se pueden entender como una serie de servidores individuales conectados uno detrás del otro. En éstos la salida de uno determinará las llegadas del siguiente.

A la hora de analizar este tipo de servicios será importante tener en cuenta que cada una de las etapas deberá tener tiempos de atención menores al tiempo entre llegadas. Esto es así a fin de evitar la saturación de alguna de ellas.

Si esto sucediese, podremos analizar distintas alternativas a implementar, por ejemplo: mejorar los ritmos promedio de servicio, reducir la variabilidad de la atención, o analizar la posibilidad de disponer múltiples servidores en paralelo. Tema que desarrollaremos a fondo en esta nota.

Así concluimos esta segunda nota de colas de espera. Hoy vimos como el mejorar el ritmo y el reducir la variabilidad de atención, nos servirán para reducir el tiempo, que nuestros clientes o productos, esperan para ser atendidos y reducir la cantidad de los mismos en la fila.

¿Pero qué hacemos cuando aun así no podemos satisfacer nuestra demanda? En la próxima nota exploraremos el caso de múltiples servidores en paralelo y sus efectos.

---