Teoría de colas: ¿Cómo gestionar las esperas?

Bienvenidos a una nueva entrada del blog de Atlas Consultora.
En este articulo vamos entender por qué las variaciones en el corto plazo de la oferta y la demanda dan lugar a la aparición de filas de espera (explicadas por la teoría de colas). También vamos analizar el impacto que genera en las organizaciones al necesitar proveer exceso de capacidad para minimizarlas.

En las últimas semanas aprendimos a medir la capacidad de nuestros procesos, a partir de los tiempos de ciclo, así como las herramientas para analizarlos, con el objetivo de mejorar su productividad. En todos estos casos asumimos que, tanto la demanda como los tiempos del proceso, son conocidos y constantes; sin embargo, ¿qué pasa cuando esto no es así? ¿qué rol juega la variabilidad a la hora de analizar nuestros procesos?

Como decíamos al inicio, las variaciones en el corto plazo de la oferta y la demanda dan lugar a la aparición de filas de espera.
Sin embargo, decidir cuánta capacidad es suficiente no es algo a tomarse a la ligera. Esto requiere de un conjunto de ideas y metodologías que permitan predecir y cuantificar este fenómeno, ya que responde a un trade-off entre costo y calidad de servicio.

¿Querés aplicar mejora continua en tu organización?
Descarga ahora la plantilla A3 PDCA Atlas y aplicá la metodología

En esta nota, nos introduciremos a la “teoría de colas o filas de espera” con el objetivo de reconocer los elementos y fundamentos de la teoría, que luego nos servirá para profundizarla en las próximas entradas del blog.

---

También te podrían interesar los siguientes artículos 📝

---

¿Por qué se generan las filas de espera de la teoría de colas?

Muchas veces tendemos a pensar que, si tenemos una capacidad superior a la demanda media, no debería formarse nunca una fila de espera, ya que eso implicaría que somos “más rápidos” para producir el bien o servicio que el ritmo al cual me lo piden. Sin embargo, como se dijo antes, eso solo es válido cuando esos tiempos y frecuencias son conocidos y constantes. La realidad es que, salvo en los casos de máquinas automáticas, difícilmente nos vayamos a encontrar con tiempos de producción constantes, y mucho menos se dará con la demanda.

Caso práctico de teoría de colas

Veamos el ejemplo de una lavandería de prendas especiales en la que todo el proceso es manual y, tanto la demanda (cantidad de cargas que son traídas por hora a la lavandería para ser lavadas) como la capacidad (cantidad de cargas que son lavadas por hora), son aleatorias con una distribución uniforme entre 1 y 6.

A simple vista, podemos ver que la lavandería lava en promedio 3,5 cargas por hora y que recibe en promedio 3,5 cargas por hora que deben ser lavadas.

Esto nos daría a pensar que, como la capacidad es igual a la demanda, nunca debería haber una carga esperando a ser lavada. Sin embargo, si simulamos con números aleatorios esta situación, veremos lo siguiente:

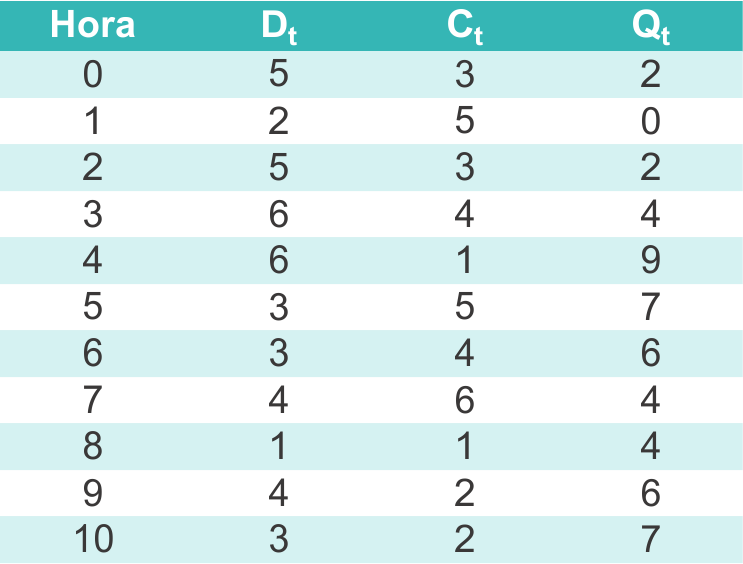
Donde:

• D_t: : es la demanda a la hora h
• C_t: : es la capacidad de la lavandería a la hora h
• Q_t: : son las cargas acumuladas (esperando a ser lavadas) a la hora h

Entonces, podemos observar que, a pesar de que la capacidad y la demanda son -en promedio- iguales, las cargas comienzan a acumularse a medida que pasan las horas. Pero esto no ocurre solo en las primeras horas; si extendemos la simulación muchas horas más, veremos lo siguiente:

Analizando la Tendencia

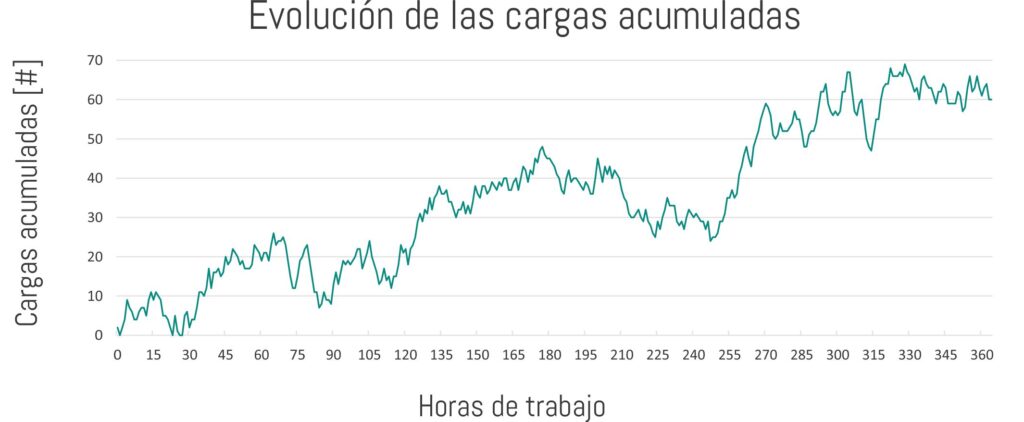
Así vemos que, si bien hay períodos en los que el sistema se “recupera” y el tamaño de la fila de espera (cantidad de cargas a la espera de ser lavadas) se reduce, la tendencia general es a que crezca.

Esto se debe, principalmente, a que no es posible stockearse de cargas procesadas (lavadas) y a la aleatoriedad misma, que no permite que se condiga siempre la capacidad con la demanda.

Ahora bien, si queremos que la fila de espera de la lavandería se redujera manteniendo las mismas características de la demanda, lo que deberíamos hacer es aumentar la capacidad, es decir, comprar más lavadoras.

Pero… ¿cuántas lavadoras sería óptimo adquirir?, ¿de qué depende esa cantidad?, ¿podemos predecir cómo quedará nuestro sistema según la cantidad de lavadoras que tengamos? En las próximas notas intentaremos dar respuesta a estas y otras preguntas más.

¿Cómo predecir las filas de espera en la teoría de colas?

Para poder calcular la capacidad adecuada de un proceso, es necesario tener en claro cuánto tiempo estamos dispuestos a dejar que nuestros clientes esperen a ser atendidos, cuán larga aceptaremos que sea la cola y cuánto estamos dispuestos a invertir/gastar para lograr esos valores.

Es por ello que, a principios del siglo pasado, un matemático llamado Agner Krarup Erlang desarrolló la ya mencionada “teoría de colas”, en la cual se estudian factores como el tiempo de espera medio en las colas o la capacidad de trabajo del sistema sin que llegue a colapsarse.

En operaciones, nos permite modelar procesos en los que varios clientes que demandan cierto servicio acuden a un mismo prestador del servicio y, por lo tanto, aparecen esperas desde que el cliente llega al sistema hasta que el prestador atiende su/s demanda/s.

Para poder entenderlo mejor y sea más fácil de identificar, vamos a definir los componentes de un sistema que puede ser analizado mediante la teoría de colas.

Componentes de un sistema de la teoría de colas

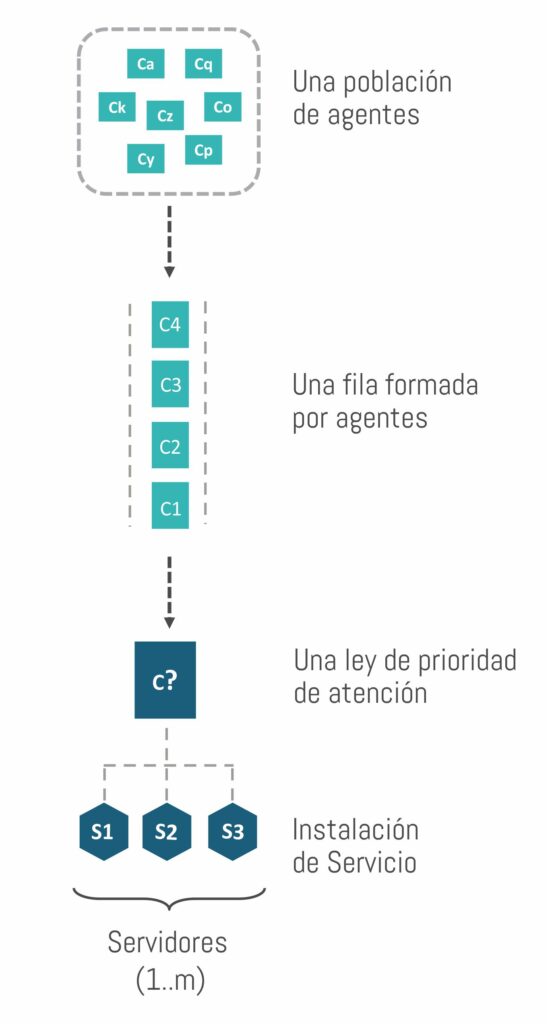
A continuación describiremos cada una brevemente.

Población

La población representa la fuente de ingresos, es decir, todas aquellas personas, productos, formularios, materiales u otro elemento susceptible de recibir el servicio que estamos analizando.
La población puede ser infinita (el número de clientes actuales en el sistema no afecta a la población) o finita (el número de clientes en el sistema afecta a la población), y los clientes pueden clasificarse en pacientes (si permanecen en la cola hasta ser atendidos) o impacientes (pueden abandonar el sistema antes de ser atendidos).

Las Filas

Son los clientes dentro del sistema a la espera de ser atendidos; un sistema puede tener una o varias filas. Las filas pueden ser independientes (cada fila es autónoma para un servicio determinado o múltiples servicios) o dependientes (una fila alimenta a la otra)

La disciplina de prioridad

Establece el próximo cliente a ser atendido. Las más utilizadas son FCFS (First Come First Serve: se atiende por orden de llegada; también conocido como FIFO), SPT (Short Processing Time: se atiende al de menor tiempo de proceso primero) y la disciplina prioritaria (permite romper el orden establecido y colocar algún cliente delante de los restantes; por ejemplo, guardias médicas, embarazadas en la cola de bancos, etc.).

Los servidores

Son las máquinas o personas capaces de brindar el servicio.

La instalación del servicio

Es el conjunto de servidores y su proceso de atención asociado; su función es contener y prestar servicios a los agentes. Está compuesta por canales (la cantidad de posibles “recorridos” que un agente puede realizar en el sistema) y fases (la cantidad de pasos en un canal). Las estructuras típicas de la instalación del servicio se pueden ver en la siguiente imagen:

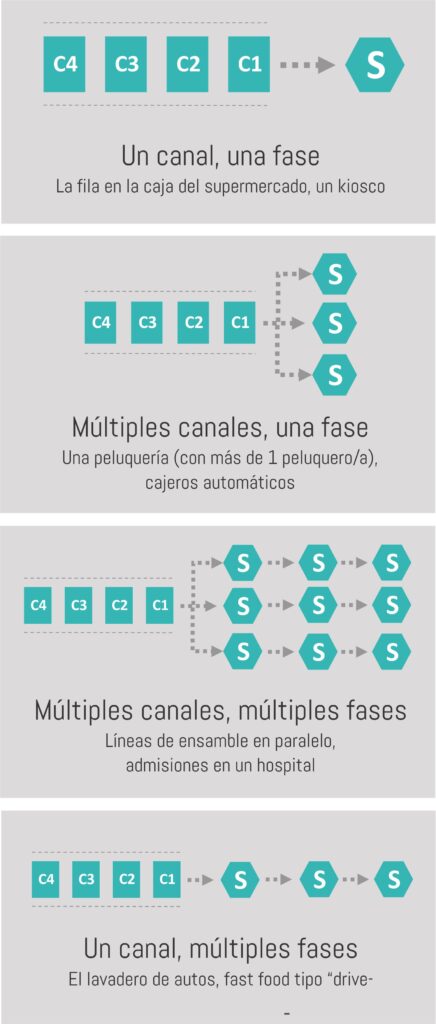
Análisis de modelos con 1 o más servidores

En las próximas semanas iremos analizando estas diferentes configuraciones, con sus respectivas particularidades, supuestos, aplicaciones y teorías asociadas.

Podés acceder desde los siguientes links a nuestros artículos donde analizamos los distintos modelos!

Campos de aplicación de las filas de espera y teoría de colas

Esta teoría se aplica principalmente en empresas de servicio o manufactura, en aquellas situaciones en las que se deba relacionar el ingreso de clientes y tiempos de servicios, en los que los ingresos y/o tiempos de servicios son variables.

Por ejemplo, líneas de montaje, cobro de facturas, call-centers, etc. Y se aplican principalmente en el análisis, diseño, modelado y prueba de sistemas con tasa variable de ingreso y servicio; en la definición de espacios y elementos variables de líneas de montaje o servicios de atención al público; en el análisis de diferentes alternativas de negocios (“what if”); y en el cálculo de los costos de pérdida por un cliente impaciente o por congestionamiento en línea de producción.

¿Podemos modelar cualquier proceso?

Si bien la mayoría de los procesos más comunes se pueden modelar y analizar mediante esta teoría, es necesario asumir ciertos supuestos:

• El ingreso de los clientes es aleatorio y se puede describir mediante una distribución del tipo Poisson, que describe la probabilidad de que n clientes lleguen en un período T de tiempo. Como puede verse en la siguiente imagen, esto implica que, cuando las llegadas de los clientes siguen una distribución Poisson, los tiempos entre llegadas (el tiempo que pasa entre la llegada de dos clientes consecutivos) tienen una distribución exponencial:

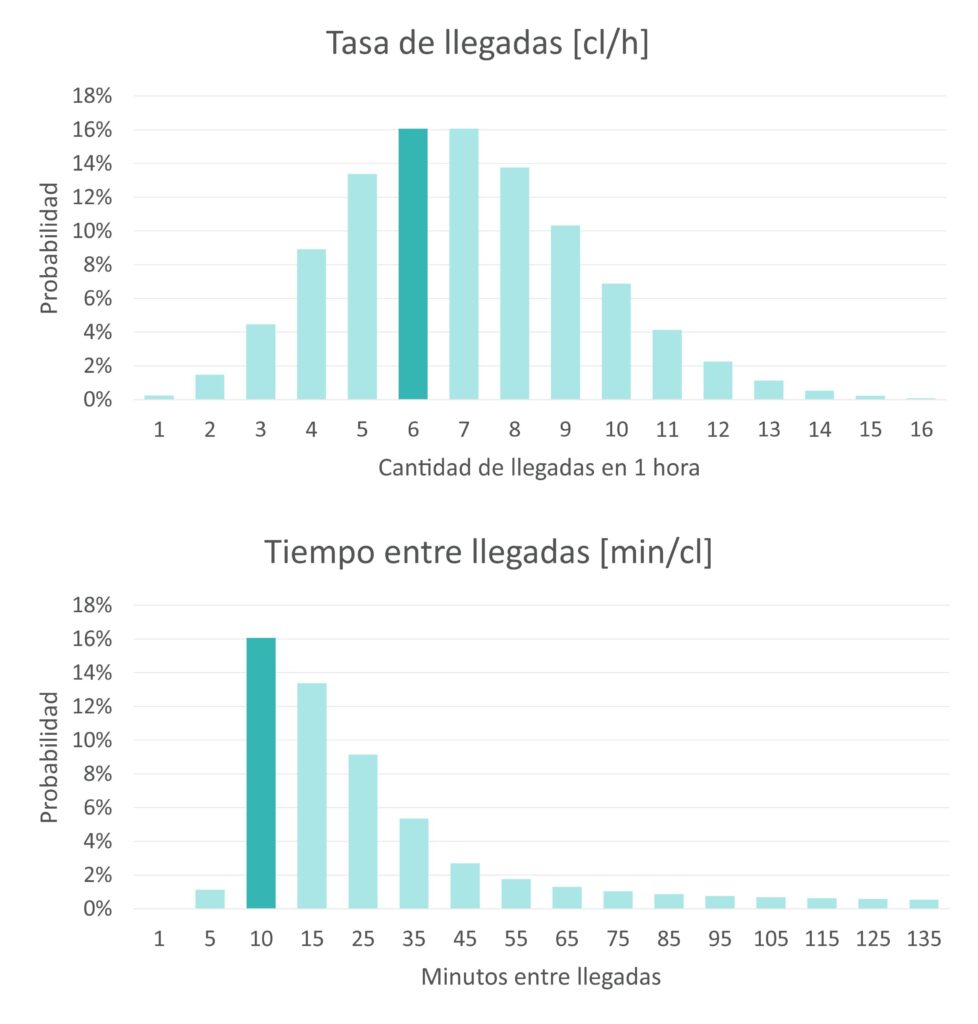
• Los tiempos de atención o prestación de servicio a los clientes se modelan mediante una distribución exponencial, que describe la probabilidad de que el tiempo de servicio del cliente no sea mayor que T períodos de tiempo.

Modelos de filas de espera

Para poder especificar los diferentes sistemas, con sus respectivas estructuras de instalación de servicios, disciplinas de ingreso de los clientes y tiempos de atención, el matemático David Kendall introdujo, en 1953, una notación que luego fue ampliada hasta lograr la configuración actual, en la forma 1/2/3 (4/5/6), donde cada uno de los números se reemplaza por lo siguiente:

1. La letra -o símbolo- que describe la disciplina de ingreso de los clientes. Si bien habitualmente asumimos distribución del tipo Poisson (se representa con la letra “M”, de Markoviano), también pueden modelarse sistemas con tiempos de llegada deterministas (se representan con la letra “D”) o con distribución general (letra “G”).
   
2. La letra -o símbolo- que describe la distribución de los tiempos de atención. Al igual que en el “1”, se utilizan las letras “M”, “D” o “G”.
   
3. La cantidad de servidores que posee el sistema. En el caso en que se estemos en proceso de diseñar o rediseñar un sistema y, por ende, la cantidad de canales de servicio no sea fijo ni conocido, entonces se debe representar con la letra “s”.
   
4. La cantidad máxima de clientes que pueden estar “dentro” del sistema (los que están esperando más los que están siendo atendidos).
   
5. Las siglas de la disciplina de prioridad. Las principales disciplinas ya fueron descritas más arriba en esta nota: FCFS, SPT, DP.
   
6. El tamaño de la población, que también fue definida anteriormente.

Las restricciones del modelo

Si bien la teoría de filas de espera es ampliamente utilizada en muchos rubros y suele dar resultados muy valiosos para las organizaciones, en algunos casos resulta algo restrictiva, ya que no es capaz de modelar todas las situaciones posibles de la realidad. Más adelante analizaremos las simulaciones computarizadas, que suelen ser la alternativa más viable cuando salimos de los supuestos de esta teoría.

Sin embargo, en las próximas semanas estudiaremos en detalle las cuatro estructuras típicas de la instalación de servicios, que nos permitirán analizar la mayoría de las situaciones en las que en nuestra organización surja la necesidad de gestionar las esperas de la forma más eficiente y rentable.

---